The inverse of the function
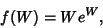 |
(1) |
also called the Omega Function. The function is implemented as the Mathematica
 (Wolfram
Research, Champaign, IL) function ProductLog[z].
(Wolfram
Research, Champaign, IL) function ProductLog[z]. 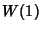 is called the Omega Constant and can be considered a
sort of ``Golden Ratio'' of exponentials since
is called the Omega Constant and can be considered a
sort of ``Golden Ratio'' of exponentials since
![\begin{displaymath}
\mathop{\rm exp}\nolimits [-W(1)]=W(1),
\end{displaymath}](l1_390.gif) |
(2) |
giving
![\begin{displaymath}
\ln\left[{1\over W(1)}\right]=W(1).
\end{displaymath}](l1_391.gif) |
(3) |
Lambert's 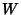 -Function has the series expansion
-Function has the series expansion
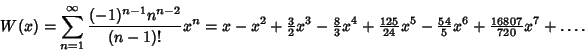 |
(4) |
The Lagrange Inversion Theorem gives the equivalent series expansion
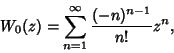 |
(5) |
where 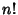 is a Factorial. However, this series oscillates between ever larger Positive and Negative values
for Real
is a Factorial. However, this series oscillates between ever larger Positive and Negative values
for Real
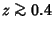 , and so cannot be used for practical numerical computation. An asymptotic
Formula which yields reasonably accurate results for
, and so cannot be used for practical numerical computation. An asymptotic
Formula which yields reasonably accurate results for
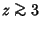 is
is
where
(Corless et al.), correcting a typographical error in de Bruijn (1961). Another expansion due to Gosper is the
Double Sum
![\begin{displaymath}
W(x)=a+\sum_{n=0}^\infty \left\{{\sum_{k=0}^n {S_1(n,k)\over...
...ight\} \left[{1-{\ln\left({x\over a}\right)\over a}}\right]^n,
\end{displaymath}](l1_406.gif) |
(9) |
where 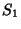 is a nonnegative Stirling Number of the First Kind and
is a nonnegative Stirling Number of the First Kind and 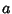 is a first approximation which can be
used to select between branches. Lambert's
is a first approximation which can be
used to select between branches. Lambert's 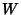 -function is two-valued for
-function is two-valued for 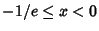 . For
. For 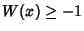 , the function is
denoted
, the function is
denoted 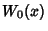 or simply
or simply 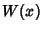 , and this is called the principal branch. For
, and this is called the principal branch. For 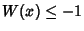 , the function is denoted
, the function is denoted
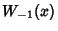 . The Derivative of
. The Derivative of 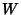 is
is
![\begin{displaymath}
W'(x)={1\over [1+W(x)]\mathop{\rm exp}\nolimits [W(x)]}={W(x)\over x[1+W(x)]}
\end{displaymath}](l1_413.gif) |
(10) |
for 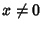 . For the principal branch when
. For the principal branch when 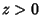 ,
,
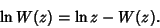 |
(11) |
See also Iterated Exponential Constants, Omega Constant
References
de Bruijn, N. G. Asymptotic Methods in Analysis. Amsterdam, Netherlands: North-Holland, pp. 27-28, 1961.
© 1996-9 Eric W. Weisstein
1999-05-26
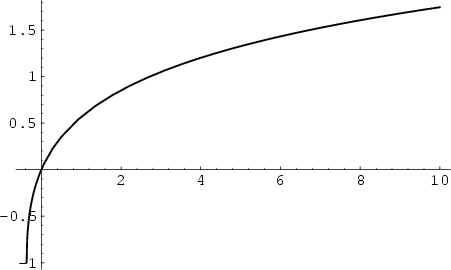
![]() -Function has the series expansion
-Function has the series expansion
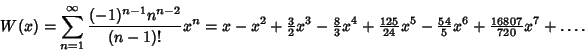
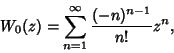
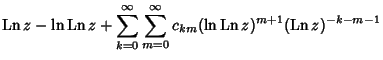
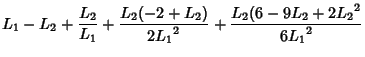
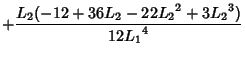
![$\displaystyle +{L_2(60-300L_2+350{L_2}^2-125{L_2}^3+12{L_2}^4)\over 60{L_1}^5}+{\mathcal O}\left[{\left({L_2\over L_1}\right)^6}\right],$](l1_401.gif)
![\begin{displaymath}
W(x)=a+\sum_{n=0}^\infty \left\{{\sum_{k=0}^n {S_1(n,k)\over...
...ight\} \left[{1-{\ln\left({x\over a}\right)\over a}}\right]^n,
\end{displaymath}](l1_406.gif)