A curve with Cartesian equation
first discussed in 1818 by Lamé. If 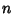 is a rational, then the curve is algebraic. However, for irrational
is a rational, then the curve is algebraic. However, for irrational 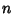 , the
curve is transcendental. For Even Integers
, the
curve is transcendental. For Even Integers 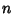 , the curve becomes closer to a rectangle as
, the curve becomes closer to a rectangle as 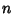 increases. For
Odd Integer values of
increases. For
Odd Integer values of 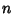 , the curve looks like the Even case in the Positive quadrant but goes to infinity
in both the second and fourth quadrants (MacTutor Archive). The Evolute of an Ellipse,
, the curve looks like the Even case in the Positive quadrant but goes to infinity
in both the second and fourth quadrants (MacTutor Archive). The Evolute of an Ellipse,
See also Astroid, Superellipse, Witch of Agnesi
References
MacTutor History of Mathematics Archive. ``Lamé Curves.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Lame.html.
© 1996-9 Eric W. Weisstein
1999-05-26