|
|
|
A nested sum over two variables. Identities involving double sums include the following:
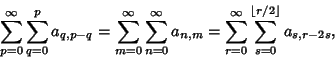 |
(1) |
| (2) |
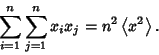 |
(3) |
Consider the sum
| (4) |
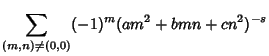 |
|||
| (5) | |||
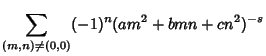 |
|||
| (6) | |||
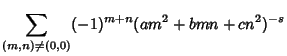 |
|||
| (7) |
| (8) |
See also Euler Sum
References
Glasser, M. L. and Zucker, I. J. ``Lattice Sums in Theoretical Chemistry.'' Theoretical Chemistry: Advances and Perspectives, Vol. 5.
New York: Academic Press, 1980.
Zucker, I. J. and Robertson, M. M. ``A Systematic Approach to the Evaluation of
![]() .'' J. Phys. A: Math. Gen. 9, 1215-1225, 1976.
.'' J. Phys. A: Math. Gen. 9, 1215-1225, 1976.
|
|
|
© 1996-9 Eric W. Weisstein