|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Euler ![]() (Le Lionnais 1983) and Eisenstein (1844) showed that the function
(Le Lionnais 1983) and Eisenstein (1844) showed that the function
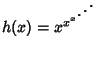 , where
, where ![]() is an abbreviation for
is an abbreviation for ![]() , converges only for
, converges only for
![]() , that is, 0.0659...
, that is, 0.0659...![]() 1.44466.... The value it converges to is the inverse of
1.44466.... The value it converges to is the inverse of ![]() , which has a closed form expression in terms of
Lambert's W-Function,
, which has a closed form expression in terms of
Lambert's W-Function,
| (1) |
| (2) |
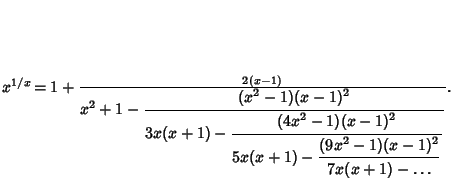
|
|
|
|
(3) |
The function
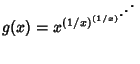 converges only for
converges only for
![]() , that is,
, that is,
![]() The value it converges to is the inverse of
The value it converges to is the inverse of ![]() .
.
Some interesting related integrals are
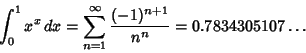 |
(4) |
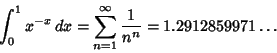 |
(5) |
See also Lambert's W-Function
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, 1972.
Baker, I. N. and Rippon, P. J. ``A Note on Complex Iteration.'' Amer. Math. Monthly 92, 501-504, 1985.
Barrows, D. F. ``Infinite Exponentials.'' Amer. Math. Monthly 43, 150-160, 1936.
Creutz, M. and Sternheimer, R. M. ``On the Convergence of Iterated Exponentiation, Part I.'' Fib. Quart.
18, 341-347, 1980.
Creutz, M. and Sternheimer, R. M. ``On the Convergence of Iterated Exponentiation, Part II.'' Fib. Quart.
19, 326-335, 1981.
de Villiers, J. M. and Robinson, P. N. ``The Interval of Convergence and Limiting Functions of a Hyperpower Sequence.''
Amer. Math. Monthly 93, 13-23, 1986.
Eisenstein, G. ``Entwicklung von
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/itrexp/itrexp.html
Khovanskii, A. N. The Application of Continued Fractions and Their Generalizations to Problems in Approximation Theory.
Groningen, Netherlands: P. Noordhoff, 1963.
Knoebel, R. A. ``Exponentials Reiterated.'' Amer. Math. Monthly 88, 235-252, 1981.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 22 and 39, 1983.
Mauerer, H. ``Über die Funktion
Spiegel, M. R. Mathematical Handbook of Formulas and Tables. New York: McGraw-Hill, 1968.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 12,
1991.
![]() .'' J. Reine angew. Math. 28, 49-52,
1844.
.'' J. Reine angew. Math. 28, 49-52,
1844.
![]() für ganzzahliges Argument (Abundanzen).''
Mitt. Math. Gesell. Hamburg 4, 33-50, 1901.
für ganzzahliges Argument (Abundanzen).''
Mitt. Math. Gesell. Hamburg 4, 33-50, 1901.
|
|
|
© 1996-9 Eric W. Weisstein