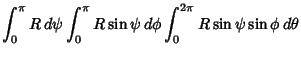The 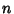 -hypersphere (often simply called the
-hypersphere (often simply called the 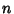 -sphere) is a generalization of the Circle (
-sphere) is a generalization of the Circle (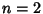 ) and
Sphere (
) and
Sphere (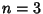 ) to dimensions
) to dimensions 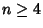 . It is therefore defined as the set of
. It is therefore defined as the set of 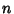 -tuples of points
(
-tuples of points
(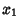 ,
, 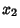 , ...,
, ..., 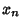 ) such that
) such that
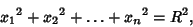 |
(1) |
where 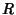 is the Radius of the hypersphere. The Content (i.e.,
is the Radius of the hypersphere. The Content (i.e., 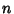 -D Volume) of an
-D Volume) of an 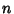 -hypersphere of
Radius
-hypersphere of
Radius 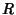 is given by
is given by
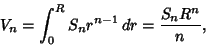 |
(2) |
where 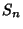 is the hyper-Surface Area of an
is the hyper-Surface Area of an 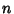 -sphere of unit radius. But, for a unit hypersphere, it must be
true that
-sphere of unit radius. But, for a unit hypersphere, it must be
true that
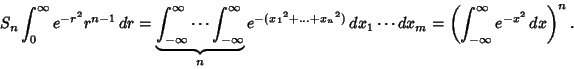 |
(3) |
But the Gamma Function can be defined by
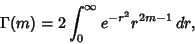 |
(4) |
so
![\begin{displaymath}
{\textstyle{1\over 2}}S_n\Gamma({\textstyle{1\over 2}}n)=[\Gamma({\textstyle{1\over 2}})]^n = (\pi^{1/2})^n
\end{displaymath}](h_2386.gif) |
(5) |
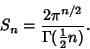 |
(6) |
This gives the Recurrence Relation
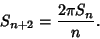 |
(7) |
Using
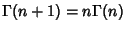 then gives
then gives
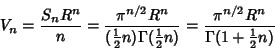 |
(8) |
(Conway and Sloane 1993).
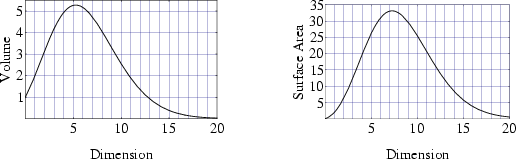
Strangely enough, the hyper-Surface Area and Content reach Maxima
and then decrease towards 0 as 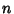 increases. The point of Maximal hyper-Surface Area satisfies
increases. The point of Maximal hyper-Surface Area satisfies
![\begin{displaymath}
{dS_n\over dn}={\pi^{n/2}[\ln\pi-\psi_0({\textstyle{1\over 2}}n)]\over\Gamma({\textstyle{1\over 2}}n)}=0,
\end{displaymath}](h_2392.gif) |
(9) |
where
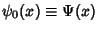 is the Digamma Function. The point of Maximal
Content satisfies
is the Digamma Function. The point of Maximal
Content satisfies
![\begin{displaymath}
{dV_n\over dn} = {\pi^{n/2} [\ln\pi-\psi_0(1+{\textstyle{1\over 2}}n)]\over 2\Gamma(1+{\textstyle{1\over 2}}n)}=0.
\end{displaymath}](h_2394.gif) |
(10) |
Neither can be solved analytically for  , but the numerical solutions are
, but the numerical solutions are
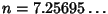 for hyper-Surface Area and
for hyper-Surface Area and
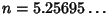 for Content. As a result, the 7-D and 5-D hyperspheres have Maximal
hyper-Surface Area and Content, respectively (Le Lionnais 1983).
for Content. As a result, the 7-D and 5-D hyperspheres have Maximal
hyper-Surface Area and Content, respectively (Le Lionnais 1983).
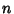 |
 |
 |
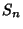 |
| 0 |
1 |
1 |
0 |
| 1 |
2 |
1 |
2 |
| 2 |
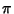 |
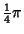 |
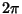 |
| 3 |
 |
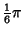 |
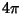 |
| 4 |
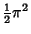 |
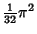 |
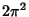 |
| 5 |
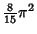 |
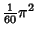 |
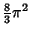 |
| 6 |
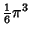 |
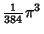 |
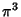 |
| 7 |
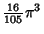 |
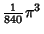 |
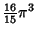 |
| 8 |
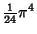 |
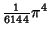 |
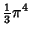 |
| 9 |
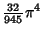 |
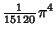 |
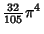 |
| 10 |
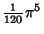 |
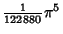 |
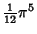 |
In 4-D, the generalization of Spherical Coordinates is defined by
The equation for a 4-sphere is
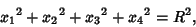 |
(15) |
and the Line Element is
![\begin{displaymath}
ds^2 = R^2[d\psi^2+\sin^2\psi (d\phi^2+\sin^2\phi\, d\theta^2)].
\end{displaymath}](h_2433.gif) |
(16) |
By defining
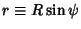 , the Line Element can be rewritten
, the Line Element can be rewritten
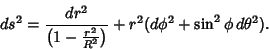 |
(17) |
The hyper-Surface Area is therefore given by
See also Circle, Hypercube, Hypersphere Packing, Mazur's Theorem,
Sphere, Tesseract
References
Conway, J. H. and Sloane, N. J. A. Sphere Packings, Lattices, and Groups, 2nd ed.
New York: Springer-Verlag, p. 9, 1993.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 58, 1983.
Peterson, I. The Mathematical Tourist: Snapshots of Modern Mathematics. New York: W. H. Freeman, pp. 96-101, 1988.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() -hypersphere (often simply called the
-hypersphere (often simply called the ![]() -sphere) is a generalization of the Circle (
-sphere) is a generalization of the Circle (![]() ) and
Sphere (
) and
Sphere (![]() ) to dimensions
) to dimensions ![]() . It is therefore defined as the set of
. It is therefore defined as the set of ![]() -tuples of points
(
-tuples of points
(![]() ,
, ![]() , ...,
, ..., ![]() ) such that
) such that
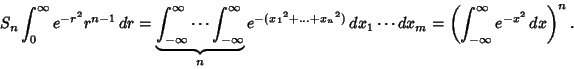
![]() increases. The point of Maximal hyper-Surface Area satisfies
increases. The point of Maximal hyper-Surface Area satisfies
![\begin{displaymath}
{dS_n\over dn}={\pi^{n/2}[\ln\pi-\psi_0({\textstyle{1\over 2}}n)]\over\Gamma({\textstyle{1\over 2}}n)}=0,
\end{displaymath}](h_2392.gif)
![\begin{displaymath}
{dV_n\over dn} = {\pi^{n/2} [\ln\pi-\psi_0(1+{\textstyle{1\over 2}}n)]\over 2\Gamma(1+{\textstyle{1\over 2}}n)}=0.
\end{displaymath}](h_2394.gif)