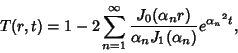To solve the Heat Conduction Equation on a 2-D disk of radius 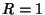 , try to separate the equation using
, try to separate the equation using
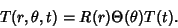 |
(1) |
Writing the 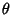 and
and 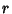 terms of the Laplacian in Spherical Coordinates gives
terms of the Laplacian in Spherical Coordinates gives
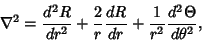 |
(2) |
so the Heat Conduction Equation becomes
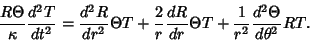 |
(3) |
Multiplying through by 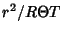 gives
gives
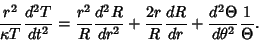 |
(4) |
The 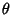 term can be separated.
term can be separated.
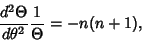 |
(5) |
which has a solution
![\begin{displaymath}
\Theta(\theta ) = A\cos\left[{\sqrt{n(n+1)}\, \theta}\right]+B\sin\left[{\sqrt{n(n+1)}\,\theta}\right].
\end{displaymath}](h_705.gif) |
(6) |
The remaining portion becomes
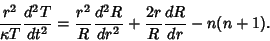 |
(7) |
Dividing by 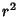 gives
gives
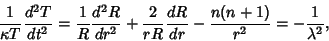 |
(8) |
where a Negative separation constant has been chosen so that the 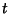 portion remains finite
portion remains finite
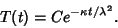 |
(9) |
The radial portion then becomes
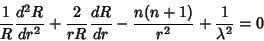 |
(10) |
![\begin{displaymath}
r^2{d^2R\over dr^2} + 2r {dR\over dr} +\left[{{r^2\over \lambda^2}-n(n+1)}\right]R=0,
\end{displaymath}](h_711.gif) |
(11) |
which is the Spherical Bessel Differential Equation. If the initial temperature is 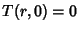 and the boundary
condition is
and the boundary
condition is 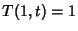 , the solution is
, the solution is
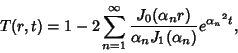 |
(12) |
where 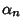 is the
is the 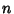 th Positive zero of the Bessel Function of the First Kind
th Positive zero of the Bessel Function of the First Kind 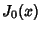 .
.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() , try to separate the equation using
, try to separate the equation using