The Bessel functions of the first kind 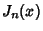 are defined as the solutions to the Bessel Differential Equation
are defined as the solutions to the Bessel Differential Equation
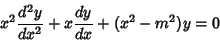 |
(1) |
which are nonsingular at the origin. They are sometimes also called Cylinder Functions or
Cylindrical Harmonics. The above plot shows  for
for 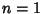 , 2, ..., 5.
, 2, ..., 5.
To solve the differential equation, apply Frobenius Method using a series solution of the form
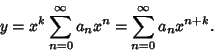 |
(2) |
Plugging into (1) yields
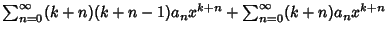
|
|
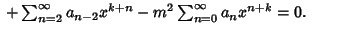
|
(4) |
The Indicial Equation, obtained by setting 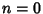 , is
, is
![\begin{displaymath}
a_0[k(k-1)+k-m^2] = a_0(k^2-m^2) = 0.
\end{displaymath}](b_781.gif) |
(5) |
Since 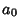 is defined as the first Nonzero term,
is defined as the first Nonzero term, 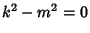 , so
, so 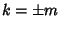 . Now, if
. Now, if 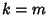 ,
,
![\begin{displaymath}
\sum_{n=0}^\infty [(m+n)(m+n-1)+(m+n)-m^2]a_nx^{m+n} + \sum_{n=2}^\infty a_{n-2}x^{m+n} = 0
\end{displaymath}](b_786.gif) |
(6) |
![\begin{displaymath}
\sum_{n=0}^\infty [(m+n)^2-m^2]a_nx^{m+n} + \sum_{n=2}^\infty a_{n-2}x^{m+n} = 0
\end{displaymath}](b_787.gif) |
(7) |
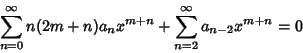 |
(8) |
![\begin{displaymath}
a_1(2m+1) + \sum_{n=2}^\infty [a_nn(2m+n)+a_{n-2}]x^{m+n} = 0.
\end{displaymath}](b_789.gif) |
(9) |
First, look at the special case 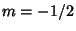 , then (9) becomes
, then (9) becomes
![\begin{displaymath}
\sum_{n=2}^\infty [a_nn(n-1)+a_{n-2}]x^{m+n} = 0,
\end{displaymath}](b_791.gif) |
(10) |
so
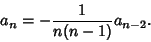 |
(11) |
Now let 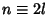 , where
, where 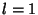 , 2, ....
, 2, ....
which, using the identity
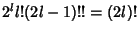 , gives
, gives
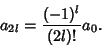 |
(13) |
Similarly, letting 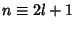
![\begin{displaymath}
a_{2l+1} &= -{1\over (2l+1)(2l)} a_{2l-1} = {(-1)^l\over [2l(2l+1)][2(l-1)(2l-1)]\cdots [2\cdot 1\cdot 3][1]} a_1,
\end{displaymath}](b_802.gif) |
(14) |
which, using the identity
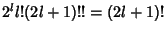 , gives
, gives
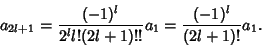 |
(15) |
Plugging back into (2) with
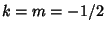 gives
gives
The Bessel Functions of order 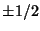 are therefore defined as
are therefore defined as
so the general solution for 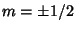 is
is
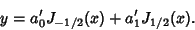 |
(19) |
Now, consider a general
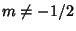 . Equation (9) requires
. Equation (9) requires
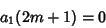 |
(20) |
![\begin{displaymath}[a_nn(2m+n)+a_{n-2}]x^{m+n} = 0
\end{displaymath}](b_821.gif) |
(21) |
for 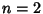 , 3, ..., so
, 3, ..., so
for 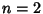 , 3, .... Let
, 3, .... Let 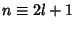 , where
, where 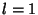 , 2, ..., then
, 2, ..., then
where 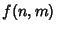 is the function of
is the function of 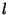 and
and 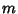 obtained by iterating the recursion relationship down to
obtained by iterating the recursion relationship down to 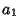 . Now let
. Now let 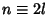 , where
, where 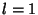 , 2, ..., so
, 2, ..., so
Plugging back into (9),
Now define
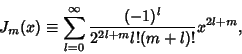 |
(27) |
where the factorials can be generalized to Gamma Functions for nonintegral 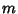 . The
above equation then becomes
. The
above equation then becomes
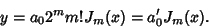 |
(28) |
Returning to equation (5) and examining the case 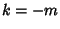 ,
,
![\begin{displaymath}
a_1(1-2m) + \sum_{n=2}^\infty [a_nn(n-2m)+a_{n-2}]x^{n-m} = 0.
\end{displaymath}](b_842.gif) |
(29) |
However, the sign of 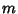 is arbitrary, so the solutions must be the same for
is arbitrary, so the solutions must be the same for 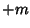 and
and 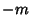 . We are therefore free to
replace
. We are therefore free to
replace 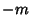 with
with 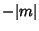 , so
, so
![\begin{displaymath}
a_1(1+2\vert m\vert) + \sum_{n=2}^\infty [a_nn(n+2\vert m\vert)+a_{n-2}]x^{\vert m\vert+n} = 0,
\end{displaymath}](b_846.gif) |
(30) |
and we obtain the same solutions as before, but with 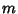 replaced by
replaced by 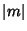 .
.
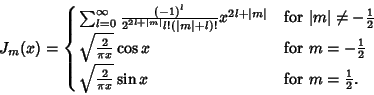 |
(31) |
We can relate 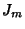 and
and 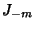 (when
(when 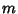 is an Integer) by writing
is an Integer) by writing
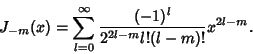 |
(32) |
Now let 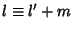 . Then
. Then
But 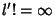 for
for
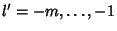 , so the Denominator is infinite and the terms on the right are zero. We
therefore have
, so the Denominator is infinite and the terms on the right are zero. We
therefore have
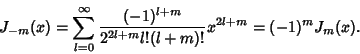 |
(34) |
Note that the Bessel Differential Equation is second-order, so there must be two linearly independent solutions.
We have found both only for 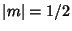 . For a general nonintegral order, the independent solutions are
. For a general nonintegral order, the independent solutions are 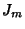 and
and
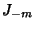 . When
. When 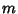 is an Integer, the general (real) solution is of the form
is an Integer, the general (real) solution is of the form
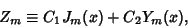 |
(35) |
where 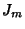 is a Bessel function of the first kind,
is a Bessel function of the first kind, 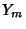 (a.k.a.
(a.k.a. 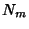 ) is the Bessel Function of the Second Kind
(a.k.a. Neumann Function or Weber Function), and
) is the Bessel Function of the Second Kind
(a.k.a. Neumann Function or Weber Function), and 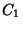 and
and 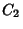 are constants. Complex
solutions are given by the Hankel Functions (a.k.a. Bessel Functions of the Third
Kind).
are constants. Complex
solutions are given by the Hankel Functions (a.k.a. Bessel Functions of the Third
Kind).
The Bessel functions are Orthogonal in ![$[0,1]$](b_863.gif) with respect to the weight factor
with respect to the weight factor 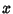 . Except
when
. Except
when 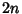 is a Negative Integer,
is a Negative Integer,
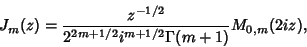 |
(36) |
where 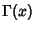 is the Gamma Function and
is the Gamma Function and 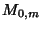 is a Whittaker Function.
is a Whittaker Function.
In terms of a Confluent Hypergeometric Function of the First Kind, the Bessel function is written
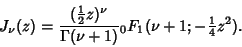 |
(37) |
A derivative identity for expressing higher order Bessel functions in terms of 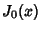 is
is
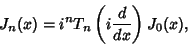 |
(38) |
where 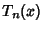 is a Chebyshev Polynomial of the First Kind. Asymptotic forms for the Bessel functions are
is a Chebyshev Polynomial of the First Kind. Asymptotic forms for the Bessel functions are
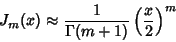 |
(39) |
for 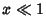 and
and
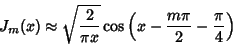 |
(40) |
for 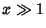 . A derivative identity is
. A derivative identity is
![\begin{displaymath}
{d\over dx} [x^mJ_m(x)] = x^mJ_{m-1}(x).
\end{displaymath}](b_874.gif) |
(41) |
An integral identity is
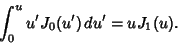 |
(42) |
Some sum identities are
![\begin{displaymath}
1 = [J_0(x)]^2+2[J_1(x)]^2+2[J_2(x)]^2+\ldots
\end{displaymath}](b_876.gif) |
(43) |
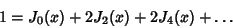 |
(44) |
and the Jacobi-Anger Expansion
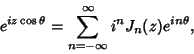 |
(45) |
which can also be written
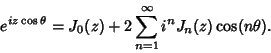 |
(46) |
The Bessel function addition theorem states
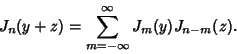 |
(47) |
Roots of the Function 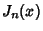 are given in the following table.
are given in the following table.
| zero |
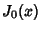 |
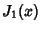 |
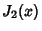 |
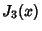 |
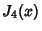 |
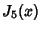 |
| 1 |
2.4048 |
3.8317 |
5.1336 |
6.3802 |
7.5883 |
8.7715 |
| 2 |
5.5201 |
7.0156 |
8.4172 |
9.7610 |
11.0647 |
12.3386 |
| 3 |
8.6537 |
10.1735 |
11.6198 |
13.0152 |
14.3725 |
15.7002 |
| 4 |
11.7915 |
13.3237 |
14.7960 |
16.2235 |
17.6160 |
18.9801 |
| 5 |
14.9309 |
16.4706 |
17.9598 |
19.4094 |
20.8269 |
22.2178 |
Let 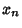 be the
be the 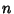 th Root of the Bessel function
th Root of the Bessel function 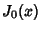 , then
, then
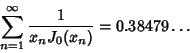 |
(48) |
(Le Lionnais 1983).
The Roots of its Derivatives are given in the following table.
| zero |
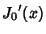 |
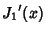 |
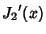 |
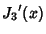 |
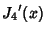 |
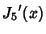 |
| 1 |
3.8317 |
1.8412 |
3.0542 |
4.2012 |
5.3175 |
6.4156 |
| 2 |
7.0156 |
5.3314 |
6.7061 |
8.0152 |
9.2824 |
10.5199 |
| 3 |
10.1735 |
8.5363 |
9.9695 |
11.3459 |
12.6819 |
13.9872 |
| 4 |
13.3237 |
11.7060 |
13.1704 |
14.5858 |
15.9641 |
17.3128 |
| 5 |
16.4706 |
14.8636 |
16.3475 |
17.7887 |
19.1960 |
20.5755 |
Various integrals can be expressed in terms of Bessel functions
which is Bessel's First Integral,
for 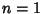 , 2, ...,
, 2, ...,
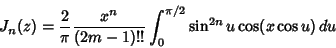 |
(53) |
for 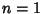 , 2, ...,
, 2, ...,
for 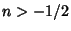 . Integrals involving
. Integrals involving 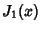 include
include
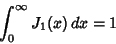 |
(55) |
![\begin{displaymath}
\int_0^\infty \left[{J_1(x)\over x}\right]^2\,dx = {4\over 3\pi}
\end{displaymath}](b_905.gif) |
(56) |
![\begin{displaymath}
\int_0^\infty \left[{J_1(x)\over x}\right]^2 x\,dx = {1\over 2}.
\end{displaymath}](b_906.gif) |
(57) |
See also Bessel Function of the Second Kind, Debye's Asymptotic Representation, Dixon-Ferrar Formula,
Hansen-Bessel Formula, Kapteyn Series, Kneser-Sommerfeld Formula, Mehler's Bessel Function
Formula, Nicholson's Formula, Poisson's Bessel Function Formula, Schläfli's Formula, Schlömilch's Series, Sommerfeld's Formula, Sonine-Schafheitlin Formula, Watson's Formula, Watson-Nicholson Formula, Weber's Discontinuous
Integrals, Weber's Formula, Weber-Sonine Formula, Weyrich's Formula
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Bessel Functions 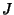 and
and 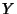 .''
§9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 358-364, 1972.
.''
§9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 358-364, 1972.
Arfken, G. ``Bessel Functions of the First Kind, 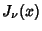 '' and ``Orthogonality.'' §11.1 and 11.2 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 573-591 and 591-596, 1985.
'' and ``Orthogonality.'' §11.1 and 11.2 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 573-591 and 591-596, 1985.
Lehmer, D. H. ``Arithmetical Periodicities of Bessel Functions.'' Ann. Math. 33, 143-150, 1932.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 25, 1983.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 619-622, 1953.
Spanier, J. and Oldham, K. B. ``The Bessel Coefficients 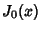 and
and 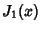 '' and ``The Bessel Function
'' and ``The Bessel Function 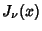 .''
Chs. 52-53 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 509-520 and 521-532, 1987.
.''
Chs. 52-53 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 509-520 and 521-532, 1987.
© 1996-9 Eric W. Weisstein
1999-05-26
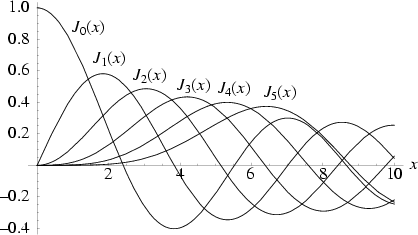
![]() are defined as the solutions to the Bessel Differential Equation
are defined as the solutions to the Bessel Differential Equation
![\begin{displaymath}
\sum_{n=0}^\infty [(m+n)(m+n-1)+(m+n)-m^2]a_nx^{m+n} + \sum_{n=2}^\infty a_{n-2}x^{m+n} = 0
\end{displaymath}](b_786.gif)
![\begin{displaymath}
\sum_{n=0}^\infty [(m+n)^2-m^2]a_nx^{m+n} + \sum_{n=2}^\infty a_{n-2}x^{m+n} = 0
\end{displaymath}](b_787.gif)
![\begin{displaymath}
a_1(2m+1) + \sum_{n=2}^\infty [a_nn(2m+n)+a_{n-2}]x^{m+n} = 0.
\end{displaymath}](b_789.gif)
![\begin{displaymath}
\sum_{n=2}^\infty [a_nn(n-1)+a_{n-2}]x^{m+n} = 0,
\end{displaymath}](b_791.gif)
![$\displaystyle {(-1)^l\over[2l(2l-1)][2(l-1)(2l-3)]\cdots[2\cdot 1\cdot 1]} a_0$](b_797.gif)
![$\displaystyle x^{-1/2}\left[{\,\sum_{n=1,3,5,\ldots}^\infty a_nx^n+\sum_{n=0,2,4,\ldots}^\infty a_nx^n}\right]$](b_808.gif)
![$\displaystyle x^{-1/2}\left[{\,\sum_{l=0}^\infty a_{2l}x^{2l}+\sum_{l=0}^\infty a_{2l+1}x^{2l+1}}\right]$](b_809.gif)
![$\displaystyle x^{-1/2}\left[{a_0 \sum_{l=0}^\infty {(-1)^l\over(2l)!} x^{2l}+a_1\sum_{l=0}^\infty {(-1)^l\over(2l+1)!}x^{2l+1}}\right]$](b_810.gif)
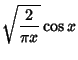
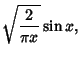
![$\displaystyle {(-1)^l\over [4l(m+l)][4(l-1)(m+l-1)]\cdots [4\cdot (m+1)]} a_0.$](b_833.gif)
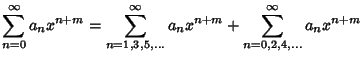
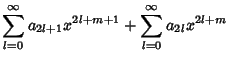
![$\displaystyle a_0 \sum_{l=0}^\infty {(-1)^l\over [4l(m+l)][4(l-1)(m+l-1)]\cdots [4\cdot (m+1)]} x^{2l+m}$](b_836.gif)
![$\displaystyle a_0 \sum_{l=0}^\infty {[(-1)^lm(m-1)\cdots 1]x^{2l+m}\over [4l(m+l)][4(l-1)(m+l-1)]\cdots [m(m-1)\cdots 1]}$](b_837.gif)
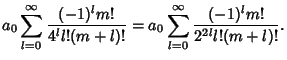
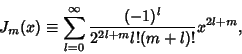
![\begin{displaymath}
a_1(1-2m) + \sum_{n=2}^\infty [a_nn(n-2m)+a_{n-2}]x^{n-m} = 0.
\end{displaymath}](b_842.gif)
![\begin{displaymath}
a_1(1+2\vert m\vert) + \sum_{n=2}^\infty [a_nn(n+2\vert m\vert)+a_{n-2}]x^{\vert m\vert+n} = 0,
\end{displaymath}](b_846.gif)
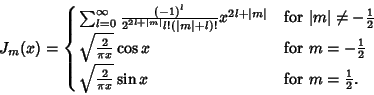
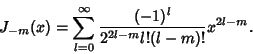
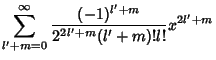
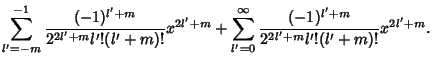
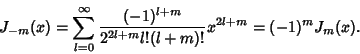
![]() . For a general nonintegral order, the independent solutions are
. For a general nonintegral order, the independent solutions are ![]() and
and
![]() . When
. When ![]() is an Integer, the general (real) solution is of the form
is an Integer, the general (real) solution is of the form
![]() with respect to the weight factor
with respect to the weight factor ![]() . Except
when
. Except
when ![]() is a Negative Integer,
is a Negative Integer,
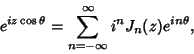
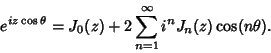
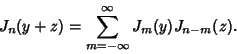
![]() are given in the following table.
are given in the following table.
![]() be the
be the ![]() th Root of the Bessel function
th Root of the Bessel function ![]() , then
, then
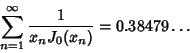
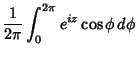
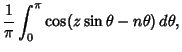
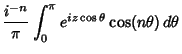
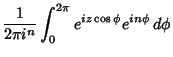
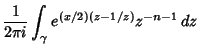
![]() and
and ![]() .''
§9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 358-364, 1972.
.''
§9.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 358-364, 1972.
![]() '' and ``Orthogonality.'' §11.1 and 11.2 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 573-591 and 591-596, 1985.
'' and ``Orthogonality.'' §11.1 and 11.2 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 573-591 and 591-596, 1985.
![]() and
and ![]() '' and ``The Bessel Function
'' and ``The Bessel Function ![]() .''
Chs. 52-53 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 509-520 and 521-532, 1987.
.''
Chs. 52-53 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 509-520 and 521-532, 1987.