|
|
|
The cylinder function is defined as
| (1) |
| (2) | |||
| (3) |
| (4) | |||
| (5) |
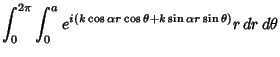 |
|||
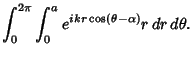 |
(6) |
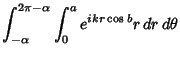 |
|||
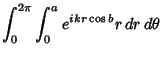 |
|||
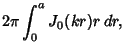 |
(7) |
![$\displaystyle {2\pi\over k^2} \int_0^{ka} J_0(u)u\,du = {2\pi\over k^2} [uJ_1(u)]_0^{ka}$](c4_1008.gif) |
|||
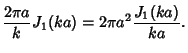 |
(8) |
As defined by Watson (1966), a ``cylinder function'' is any function which satisfies the
Recurrence Relations
| (9) |
| (10) |
See also Bessel Function of the First Kind, Cylinder Function, Cylindrical Function, Hemispherical Function
References
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University
Press, 1966.
|
|
|
© 1996-9 Eric W. Weisstein