|
|
|
The four parameters ![]() ,
, ![]() ,
, ![]() , and
, and ![]() describing a finite rotation about an arbitrary axis. The
Euler parameters are defined by
describing a finite rotation about an arbitrary axis. The
Euler parameters are defined by
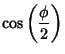 |
(1) | ||
![$\displaystyle \left[\begin{array}{c}e_1\\ e_2\\ e_3\end{array}\right] = \hat {\bf n} \sin\left({\phi\over 2}\right),$](e_2314.gif) |
(2) |
| (3) |
Because Euler's Rotation Theorem states that an arbitrary rotation may be described by only three parameters, a
relationship must exist between these four quantities
| (4) |
| (5) |
| (6) |
The Euler parameters may be given in terms of the Euler Angles by
| (7) | |||
| (8) | |||
| (9) | |||
| (10) |
Using the Euler parameters, the Rotation Formula becomes
| (11) |
![\begin{displaymath}
\left[{\matrix{x'\cr y'\cr z'\cr}}\right] = {\hbox{\sf A}}\left[{\matrix{x\cr y\cr z\cr}}\right],
\end{displaymath}](e_2327.gif) |
(12) |
| (13) |
| (14) | |||
| (15) | |||
| (16) | |||
| (17) | |||
| (18) | |||
| (19) | |||
| (20) | |||
| (21) | |||
| (22) |
See also Euler Angles, Quaternion, Rotation Matrix
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 198-200, 1985.
Goldstein, H. Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, 1980.
Landau, L. D. and Lifschitz, E. M. Mechanics, 3rd ed. Oxford, England: Pergamon Press, 1976.
|
|
|
© 1996-9 Eric W. Weisstein