|
|
|
When discussing a Rotation, there are two possible conventions: rotation of the axes and rotation of the object relative to fixed axes.
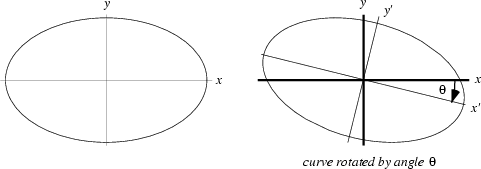
In ![]() , let a curve be rotated by a clockwise Angle
, let a curve be rotated by a clockwise Angle ![]() , so that the original axes of the curve are
, so that the original axes of the curve are
![]() and
and ![]() , and the new axes of the curve are
, and the new axes of the curve are ![]() and
and ![]() . The Matrix
transforming the original curve to the rotated curve, referred to the original
. The Matrix
transforming the original curve to the rotated curve, referred to the original ![]() and
and ![]() axes, is
axes, is
| (1) |
| (2) |
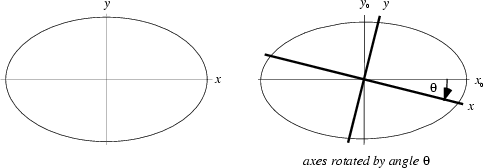
On the other hand, let the axes with respect to which a curve is measured be rotated by a clockwise Angle
![]() , so that the original axes are
, so that the original axes are ![]() and
and ![]() , and the new axes are
, and the new axes are ![]() and
and ![]() . Then the Matrix transforming the coordinates of the curve with respect to
. Then the Matrix transforming the coordinates of the curve with respect to ![]() and
and ![]() is
given by the Matrix Transpose of the above matrix:
is
given by the Matrix Transpose of the above matrix:
| (3) |
| (4) |
In ![]() , rotations of the
, rotations of the ![]() -,
-, ![]() -, and
-, and ![]() -axes give the matrices
-axes give the matrices
![$\displaystyle \left[\begin{array}{ccc}1 & 0 & 0\\ 0 & \cos\alpha & \sin\alpha\\ 0 & -\sin\alpha & \cos\alpha\end{array}\right]$](r_2027.gif) |
(5) | ||
![$\displaystyle \left[\begin{array}{ccc}\cos\beta & 0 & -\sin\beta\\ 0 & 1 & 0\\ \sin\beta & 0 & \cos\beta\end{array}\right]$](r_2029.gif) |
(6) | ||
![$\displaystyle \left[\begin{array}{ccc}\cos\gamma & \sin\gamma & 0\\ -\sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1\end{array}\right].$](r_2031.gif) |
(7) |
See also Euler Angles, Euler's Rotation Theorem, Rotation
|
|
|
© 1996-9 Eric W. Weisstein