|
|
|
An ![]() -gonal cupola
-gonal cupola ![]() (possible for only
(possible for only ![]() , 4, 5) is a Polyhedron having
, 4, 5) is a Polyhedron having ![]() Triangular and
Triangular and
![]() Square faces separating an
Square faces separating an ![]() and a
and a ![]() Regular Polygon. The coordinates of the base
Vertices are
Regular Polygon. The coordinates of the base
Vertices are
| (1) |
| (2) |
| (3) | |||
| (4) |
![$\displaystyle \left[\begin{array}{c}R\cos\left({\pi\over 2n}\right)\\ R\sin\left({\pi\over 2n}\right)\\ 0\end{array}\right]$](c4_470.gif) |
(5) | ||
| (6) |
| (7) |
| (8) |
| (9) |
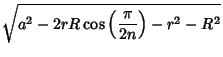 |
|||
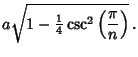 |
(10) |
See also Bicupola, Elongated Cupola, Gyroelongated Cupola, Pentagonal Cupola, Square Cupola, Triangular Cupola
References
Johnson, N. W. ``Convex Polyhedra with Regular Faces.'' Canad. J. Math. 18, 169-200, 1966.
|
|
|
© 1996-9 Eric W. Weisstein