|
|
|
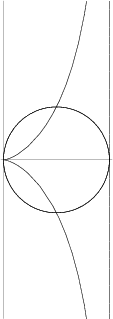
A curve invented by Diocles in about 180 BC ![]() in connection with his attempt to duplicate the cube by geometrical
methods. The name ``cissoid'' first appears in the work of Geminus about 100 years later. Fermat
in connection with his attempt to duplicate the cube by geometrical
methods. The name ``cissoid'' first appears in the work of Geminus about 100 years later. Fermat ![]() and Roberval
constructed the tangent in 1634. Huygens
and Roberval
constructed the tangent in 1634. Huygens ![]() and Wallis found, in 1658, that the Area between the curve and its
asymptote was
and Wallis found, in 1658, that the Area between the curve and its
asymptote was ![]() (MacTutor Archive). From a given point there are either one or three Tangents to
the cissoid.
(MacTutor Archive). From a given point there are either one or three Tangents to
the cissoid.
Given an origin ![]() and a point
and a point ![]() on the curve, let
on the curve, let ![]() be the point where the extension of the line
be the point where the extension of the line ![]() intersects the
line
intersects the
line ![]() and
and ![]() be the intersection of the Circle of Radius
be the intersection of the Circle of Radius ![]() and center
and center ![]() with the extension of
with the extension of
![]() . Then the cissoid of Diocles is the curve which satisfies
. Then the cissoid of Diocles is the curve which satisfies ![]() .
.
The cissoid of Diocles is the Roulette of the Vertex of a Parabola rolling on an
equal Parabola. Newton ![]() gave a method of drawing the cissoid of Diocles using two line segments of equal
length at Right Angles. If they are moved so that one line always passes through a fixed point and the
end of the other line segment slides along a straight line, then the Midpoint of the sliding line segment traces out a
cissoid of Diocles.
gave a method of drawing the cissoid of Diocles using two line segments of equal
length at Right Angles. If they are moved so that one line always passes through a fixed point and the
end of the other line segment slides along a straight line, then the Midpoint of the sliding line segment traces out a
cissoid of Diocles.
The cissoid of Diocles is given by the parametric equations
| (1) | |||
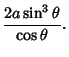 |
(2) |
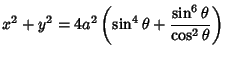 |
|||
| (3) |
| (4) |
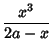 |
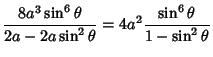 |
||
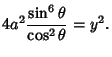 |
(5) |
| (6) |
Using the alternative parametric form
| (7) | |||
| (8) |
| (9) |
References
Gray, A. ``The Cissoid of Diocles.'' §3.4 in
Modern Differential Geometry of Curves and Surfaces.Boca Raton, FL: CRC Press, pp. 43-46, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 98-100, 1972.
Lee, X. ``Cissoid of Diocles.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/CissoidOfDiocles_dir/cissoidOfDiocles.html.
Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, pp. 130-133, 1967.
MacTutor History of Mathematics Archive. ``Cissoid of Diocles.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Cissoid.html.
Yates, R. C. ``Cissoid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 26-30, 1952.
|
|
|
© 1996-9 Eric W. Weisstein