|
|
|
There are four Circles that touch all the sides of a given Triangle. These are all touched by the Circle through the intersection of the Angle Bisectors of the Triangle, known as the Nine-Point Circle.
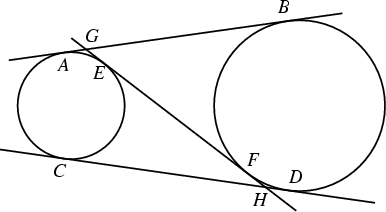
Given the above figure, ![]() , since
, since
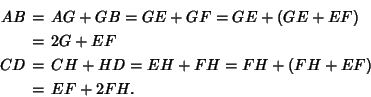
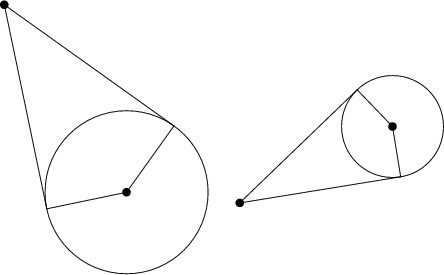
The line tangent to a Circle of Radius ![]() centered at
centered at ![]()
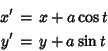
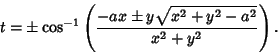
See also Kissing Circles Problem, Miquel Point, Monge's Problem, Pedal Circle, Tangent Line, Triangle
References
Dixon, R. Mathographics. New York: Dover, p. 21, 1991.
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 4-5, 1991.