|
|
|
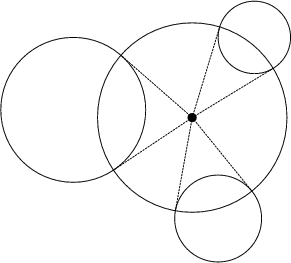
Draw a Circle that cuts three given Circles Perpendicularly. The solution
is obtained by drawing the Radical Center ![]() of the given three Circles. If it lies outside the
three Circles, then the Circle with center
of the given three Circles. If it lies outside the
three Circles, then the Circle with center ![]() and Radius formed by the tangent from
and Radius formed by the tangent from ![]() to one of the
given Circles intersects the given Circles perpendicularly. Otherwise, if
to one of the
given Circles intersects the given Circles perpendicularly. Otherwise, if ![]() lies
inside one of the circles, the problem is unsolvable.
lies
inside one of the circles, the problem is unsolvable.
See also Circle Tangents, Radical Center
References
Dörrie, H. ``Monge's Problem.'' §31 in 100 Great Problems of Elementary Mathematics: Their History and Solutions.
New York: Dover, pp. 151-154, 1965.