|
|
|
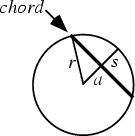
The Line Segment joining two points on a curve. The term is often used to describe a Line Segment whose
ends lie on a Circle. In the above figure, ![]() is the Radius of the Circle,
is the Radius of the Circle, ![]() is called the
Apothem, and
is called the
Apothem, and ![]() the Sagitta.
the Sagitta.
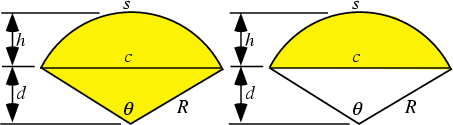
The shaded region in the left figure is called a Sector, and the shaded region in the right figure is called a Segment.
All Angles inscribed in a Circle and subtended by the same chord are equal. The converse is also true: The Locus of all points from which a given segment subtends equal Angles is a Circle.
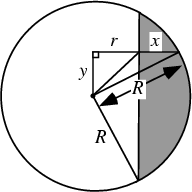
Let a Circle of Radius ![]() have a Chord at distance
have a Chord at distance ![]() . The Area enclosed by the Chord, shown
as the shaded region in the above figure, is then
. The Area enclosed by the Chord, shown
as the shaded region in the above figure, is then
| (1) |
| (2) |
| (3) |
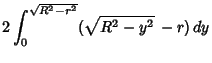 |
|||
![$\displaystyle \left[{y\sqrt{R^2-y^2}+R^2\tan^{-1}\left({y\over\sqrt{R^2-y^2}}\right)-2ry}\right]_0^{\sqrt{R^2-r^2}}$](c1_1599.gif) |
|||
![$\displaystyle r\sqrt{R^2-r^2}+R^2\tan^{-1}\left[{\left({R\over r}\right)^2-1}\right]-2r\sqrt{R^2-r^2}$](c1_1600.gif) |
|||
![$\displaystyle R^2\tan^{-1}\left[{\left({R\over r}\right)^2-1}\right]-r\sqrt{R^2-r^2}.$](c1_1601.gif) |
(4) |
| (5) |
See also Annulus, Apothem, Bertrand's Problem, Concentric Circles, Radius, Sagitta, Sector, Segment
|
|
|
© 1996-9 Eric W. Weisstein