|
|
|
The equation which is solved to find a Matrix's Eigenvalues, also called the
Characteristic Polynomial. Given a ![]() system of equations with Matrix
system of equations with Matrix
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
![\begin{displaymath}
\left[{\matrix{a_{11} & a_{12} & \ldots & a_{1k}\cr
a_{21} ...
...ts & \vdots\cr
a_{k1} & a_{k2} & \ldots & a_{kk}\cr}}\right],
\end{displaymath}](c1_1222.gif) |
(6) |
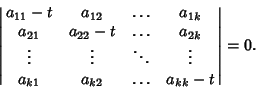 |
(7) |
See also Ballieu's Theorem, Cayley-Hamilton Theorem, Parodi's Theorem, Routh-Hurwitz Theorem
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1117-1119, 1979.