Calabi's Triangle

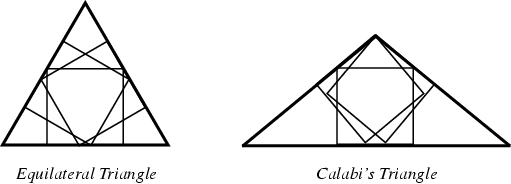
$\begin{figure}\begin{center}\BoxedEPSF{CalabisTriangle.epsf scaled 901}\end{center}\end{figure}$

The one Triangle in addition to the Equilateral Triangle for which the largest inscribed Square can be inscribed in three different ways. The ratio of the sides to that of the base is given by $x=1.55138752454\ldots$ (Sloane's A046095), where

$\begin{displaymath} x={1\over 3}+{(-23+3i\sqrt{237}\,)^{1/3}\over 3\cdot 2^{2/3}}+{11\over 3[2(-23+3i\sqrt{237}\,)]^{1/3}} \end{displaymath}$

is the largest Positive Root of

$\begin{displaymath} 2x^3-2x^2-3x+2=0, \end{displaymath}$

which has Continued Fraction [1, 1, 1, 4, 2, 1, 2, 1, 5, 2, 1, 3, 1, 1, 390, ...] (Sloane's A046096).

See also Graham's Biggest Little Hexagon

References

Conway, J. H. and Guy, R. K. ``Calabi's Triangle.'' In The Book of Numbers. New York: Springer-Verlag, p. 206, 1996.

Sloane, N. J. A. A046095 and A046096 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.