|
|
|
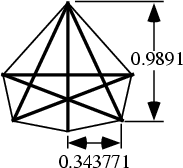
The largest possible (not necessarily regular) Hexagon for which no two of the corners are more than unit distance
apart. In the above figure, the heavy lines are all of unit length. The Area of the hexagon is
![]() ,
where
,
where ![]() is the second-largest real Root of
is the second-largest real Root of
|
|
|
|
|
See also Calabi's Triangle
References
Conway, J. H. and Guy, R. K. ``Graham's Biggest Little Hexagon.'' In The Book of Numbers. New York:
Springer-Verlag, pp. 206-207, 1996.
Graham, R. L. ``The Largest Small Hexagon.'' J. Combin. Th. Ser. A 18, 165-170, 1975.