|
|
|
An incidence system (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ) in which a set
) in which a set ![]() of
of ![]() points is partitioned into a family
points is partitioned into a family ![]() of
of
![]() subsets (blocks) in such a way that any two points determine
subsets (blocks) in such a way that any two points determine ![]() blocks with
blocks with ![]() points in each block, and
each point is contained in
points in each block, and
each point is contained in ![]() different blocks. It is also generally required that
different blocks. It is also generally required that ![]() , which is where the
``incomplete'' comes from in the formal term most often encountered for block designs, Balanced Incomplete Block
Designs (BIBD). The five parameters are not independent, but satisfy the two relations
, which is where the
``incomplete'' comes from in the formal term most often encountered for block designs, Balanced Incomplete Block
Designs (BIBD). The five parameters are not independent, but satisfy the two relations
| (1) |
| (2) |
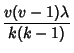 |
(3) | ||
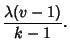 |
(4) |
Writing
![]() and
and
![]() , then the Incidence Matrix of the BIBD is given by the
, then the Incidence Matrix of the BIBD is given by the ![]() Matrix
Matrix
![]() defined by
defined by
| (5) |
| (6) |
Examples of BIBDs are given in the following table.
| Block Design | ( |
| Affine Plane | ( |
| Fano Plane | (7, 3, 1)) |
| Hadamard Design | Symmetric ( |
| Projective Plane | Symmetric ( |
| Steiner Triple System | ( |
| Unital | ( |
See also Affine Plane, Design, Fano Plane, Hadamard Design, Parallel Class, Projective Plane, Resolution, Resolvable, Steiner Triple System, Symmetric Block Design, Unital
References
Dinitz, J. H. and Stinson, D. R. ``A Brief Introduction to Design Theory.'' Ch. 1 in
Contemporary Design Theory: A Collection of Surveys (Ed. J. H. Dinitz and
D. R. Stinson). New York: Wiley, pp. 1-12, 1992.
Ryser, H. J. ``The
![]() -Configuration.'' §8.1 in
Combinatorial Mathematics. Buffalo, NY: Math. Assoc. Amer., pp. 96-102, 1963.
-Configuration.'' §8.1 in
Combinatorial Mathematics. Buffalo, NY: Math. Assoc. Amer., pp. 96-102, 1963.
|
|
|
© 1996-9 Eric W. Weisstein