|
|
|
For a ![]() -D Polytope
-D Polytope ![]() , the incidence matrix is defined by
, the incidence matrix is defined by
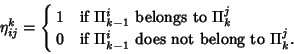
| 1 | ||||
| 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 |
| 1 | |
| 1 | |
| 1 | |
| 1 |
See also Adjacency Matrix, k-Chain, k-Circuit
|
|
|
© 1996-9 Eric W. Weisstein