Steiner Triple System

Let $X$ be a set of $v\geq 3$ elements together with a set $B$ of 3-subset (triples) of $X$ such that every 2-Subset of $X$ occurs in exactly one triple of $B$. Then $B$ is called a Steiner triple system and is a special case of a Steiner System with $t=2$ and $k=3$. A Steiner triple system $S(v)=S(v,k=3,\lambda=1)$ of order $v$ exists Iff $v\equiv 1, 3\ \left({{\rm mod\ } {6}}\right)$ (Kirkman 1847). In addition, if Steiner triple systems $S_1$ and $S_2$ of orders $v_1$ and $v_2$ exist, then so does a Steiner triple system $S$ of order $v_1v_2$ (Ryser 1963, p. 101).

Examples of Steiner triple systems $S(v)$ of small orders $v$ are

$$S_3 = \{\{1, 2, 3\}\}$$

$$S_7 = \{\{1, 2, 4\}, \{2, 3, 5\}, \{3, 4, 6\}, \{4, 5, 7\},$$

$$\phantom{=} \{5, 6, 1\}, \{6, 7, 2\}, \{7, 1, 3\}\}$$

$$S_9 = \{\{1, 2, 3\}, \{4, 5, 6\}, \{7, 8, 9\}, \{1, 4, 7\},$$

$$\phantom{=} \{2, 5, 8\}, \{3, 6, 9\}, \{1, 5, 9\}, \{2, 6, 7\}$$

$$\phantom{=} \{3, 4, 8\}, \{1, 6, 8\}, \{2, 4, 9\}, \{3, 5, 7\}\}.$$

The number of nonisomorphic Steiner triple systems $S(v)$ of orders $v=7$, 9, 13, 15, 19, ... (i.e., $6k+1,3$) are 1, 1, 2, 80, $>1.1\times 10^9$, ... (Colbourn and Dinitz 1996, pp. 14-15; Sloane's A030129). $S(7)$ is the same as the finite Projective Plane of order 2. $S(9)$ is a finite Affine Plane which can be constructed from the array

$$\matrix{a & b & c\cr d & e & f\cr g & h & i\cr}.$$

One of the two $S(13)$s is a finite Hyperbolic Plane. The 80 Steiner triple systems $S(15)$ have been studied by Tonchev and Weishaar (1997). There are more than $1.1\times 10^9$ Steiner triple systems of order 19 (Stinson and Ferch 1985; Colbourn and Dinitz 1996, p. 15).

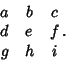
See also Hadamard Matrix, Kirkman Triple System, Steiner Quadruple System, Steiner System

References

Colbourn, C. J. and Dinitz, J. H. (Eds.) ``Steiner Triple Systems.'' §4.5 in CRC Handbook of Combinatorial Designs. Boca Raton, FL: CRC Press, pp.14-15 and 70, 1996.

Kirkman, T. P. ``On a Problem in Combinatorics.'' Cambridge Dublin Math. J. 2, 191-204, 1847.

Lindner, C. C. and Rodger, C. A. Design Theory. Boca Raton, FL: CRC Press, 1997.

Ryser, H. J. Combinatorial Mathematics. Buffalo, NY: Math. Assoc. Amer., pp. 99-102, 1963.

Sloane, N. J. A. Sequence A030129 in ``The On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html.

Stinson, D. R. and Ferch, H. ``2000000 Steiner Triple Systems of Order 19.'' Math. Comput. 44, 533-535, 1985.

Tonchev, V. D. and Weishaar, R. S. ``Steiner Triple Systems of Order 15 and Their Codes.'' J. Stat. Plan. Inference 58, 207-216, 1997.