|
|
|
Watson's (1966, pp. 188-190) definition of an Airy function is the solution to the Airy Differential Equation
| (1) |
| (2) |
![$\displaystyle {\textstyle{1\over 3}}\pi \sqrt{{\textstyle{x\over 3}}}
\left[{J_...
...^{3/2}\over 3^{3/2}}\right)+J_{1/3}\left({2x^{3/2}\over 3^{3/2}}\right)}\right]$](a_498.gif) |
|||
| (3) | |||
![$\displaystyle {\textstyle{1\over 3}}\pi \sqrt{{\textstyle{x\over 3}}}
\left[{I_...
...{3/2}\over 3^{3/2}}\right)-I_{1/3}\left({2x^{3/2}\over 3^{3/2}}\right)}\right],$](a_500.gif) |
|||
| (4) |
| (5) |
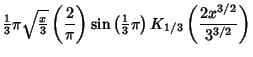 |
(6) | ||
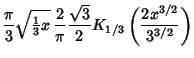 |
(7) | ||
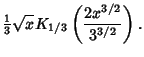 |
(8) |
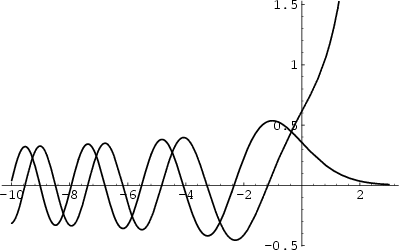
A more commonly used definition of Airy functions is given by Abramowitz and Stegun (1972, pp. 446-447) and illustrated
above. This definition identifies the
![]() and
and
![]() functions as the two Linearly Independent
solutions to (1) with
functions as the two Linearly Independent
solutions to (1) with ![]() and a Minus Sign,
and a Minus Sign,
| (9) |
| (10) |
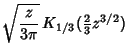 |
(11) | ||
![$\displaystyle \sqrt{z\over 3} \,[I_{-1/3}({\textstyle{2\over 3}}z^{3/2})+I_{1/3}({\textstyle{2\over 3}}z^{3/2})].$](a_515.gif) |
(12) |
| (13) |
| (14) |
The Asymptotic Series of
![]() has a different form in different Quadrants of the
Complex Plane, a fact known as the Stokes Phenomenon. Functions related to the Airy functions have been
defined as
has a different form in different Quadrants of the
Complex Plane, a fact known as the Stokes Phenomenon. Functions related to the Airy functions have been
defined as
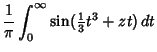 |
(15) | ||
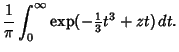 |
(16) |
See also Airy-Fock Functions
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Airy Functions.''
§10.4 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 446-452, 1972.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Bessel Functions of Fractional Order, Airy Functions, Spherical Bessel Functions.'' §6.7 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 234-245, 1992.
Spanier, J. and Oldham, K. B. ``The Airy Functions Ai(
Watson, G. N. A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University
Press, 1966.
![]() ) and Bi(
) and Bi(![]() ).''
Ch. 56 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 555-562, 1987.
).''
Ch. 56 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 555-562, 1987.
|
|
|
© 1996-9 Eric W. Weisstein