Some authors define a general Airy differential equation as
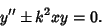 |
(1) |
This equation can be solved by series solution using the expansions
Specializing to the ``conventional'' Airy differential equation occurs by taking the Minus Sign and setting
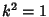 . Then plug (4) into
. Then plug (4) into
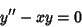 |
(5) |
to obtain
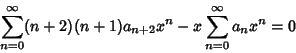 |
(6) |
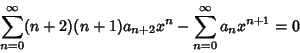 |
(7) |
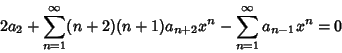 |
(8) |
![\begin{displaymath}
2a_2 + \sum_{n=1}^\infty [(n+2)(n+1) a_{n+2}-a_{n-1}]x^n = 0.
\end{displaymath}](a_447.gif) |
(9) |
In order for this equality to hold for all 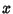 , each term must separately be 0. Therefore,
, each term must separately be 0. Therefore,
Starting with the 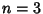 term and using the above Recurrence Relation, we obtain
term and using the above Recurrence Relation, we obtain
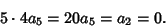 |
(12) |
Continuing, it follows by Induction that
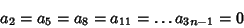 |
(13) |
for 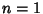 , 2, .... Now examine terms of the form
, 2, .... Now examine terms of the form 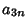 .
.
Again by Induction,
![\begin{displaymath}
a_{3n} = {{a_0} \over {[(3n)(3n-1)][(3n-3)(3n-4)]\cdots [6 \cdot 5][3 \cdot 2]}}
\end{displaymath}](a_461.gif) |
(17) |
for 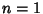 , 2, .... Finally, look at terms of the form
, 2, .... Finally, look at terms of the form 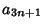 ,
,
By Induction,
![\begin{displaymath}
a_{3n+1} = {{a_1} \over {[(3n+1)(3n)][(3n-2)(3n-3)] \cdots [7 \cdot 6][4 \cdot 3]}}
\end{displaymath}](a_469.gif) |
(21) |
for 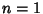 , 2, .... The general solution is therefore
, 2, .... The general solution is therefore
![$y = a_0\left[{1+\sum_{n=1}^\infty{{x^{3n}}\over{(3n)(3n-1)(3n-3)(3n-4)\cdots3\cdot2}}}\right]$](a_470.gif)
|
|
![${}+a_1\left[{x+\sum_{n=1}^\infty{{x^{3n+1}}\over{(3n+1)(3n)(3n-2)(3n-3)\cdots4\cdot3}}}\right].$](a_471.gif)
|
|
|
|
(22) |
For a general 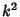 with a Minus Sign, equation (1) is
with a Minus Sign, equation (1) is
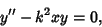 |
(23) |
and the solution is
![\begin{displaymath}
y(x)= {\textstyle{1\over 3}}\sqrt{x}\left[{AI_{-1/3}\left({{...
...I_{1/3}\left({{\textstyle{2\over 3}} kx^{3/2}}\right)}\right],
\end{displaymath}](a_474.gif) |
(24) |
where 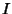 is a Modified Bessel Function of the First Kind. This is usually expressed in terms of the Airy
Functions
is a Modified Bessel Function of the First Kind. This is usually expressed in terms of the Airy
Functions
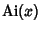 and
and
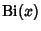
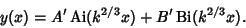 |
(25) |
If the Plus Sign is present instead, then
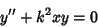 |
(26) |
and the solutions are
![\begin{displaymath}
y(x)= {\textstyle{1\over 3}}\sqrt{x}\left[{AJ_{-1/3}\left({{...
...J_{1/3}\left({{\textstyle{2\over 3}} kx^{3/2}}\right)}\right],
\end{displaymath}](a_480.gif) |
(27) |
where 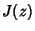 is a Bessel Function of the First Kind.
is a Bessel Function of the First Kind.
See also Airy-Fock Functions, Airy Functions, Bessel Function of the First Kind, Modified Bessel
Function of the First Kind
© 1996-9 Eric W. Weisstein
1999-05-25
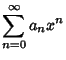
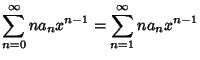
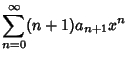
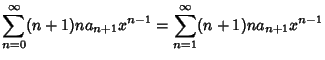
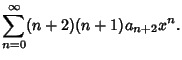
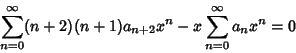
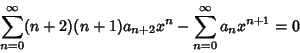
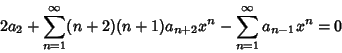
![\begin{displaymath}
2a_2 + \sum_{n=1}^\infty [(n+2)(n+1) a_{n+2}-a_{n-1}]x^n = 0.
\end{displaymath}](a_447.gif)