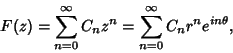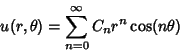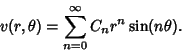Given a Taylor Series
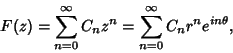 |
(1) |
where the Complex Number 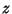 has been written in the polar form
has been written in the polar form
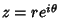 , examine
the Real and Imaginary Parts
, examine
the Real and Imaginary Parts
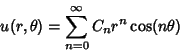 |
(2) |
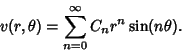 |
(3) |
Abel's theorem states that, if 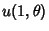 and
and 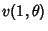 are Convergent, then
are Convergent, then
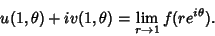 |
(4) |
Stated in words, Abel's theorem guarantees that, if a Real Power Series Converges
for some Positive value of the argument, the Domain of Uniform Convergence extends at least up to and
including this point. Furthermore, the continuity of the sum function extends at least up to and including this point.
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 773, 1985.
© 1996-9 Eric W. Weisstein
1999-05-25