|
|
|
A Series
![]() is uniformly convergent to
is uniformly convergent to ![]() for a set
for a set ![]() of values of
of values of ![]() if, for each
if, for each
![]() , an Integer
, an Integer ![]() can be found such that
can be found such that
| (1) |
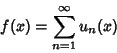 |
(2) |
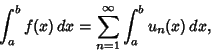 |
(3) |
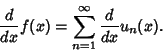 |
(4) |
See also Abel's Theorem, Abel's Uniform Convergence Test, Weierstraß M-Test
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 299-301, 1985.