The set of 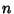 quantities
quantities 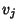 are components of an
are components of an 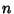 -D Vector
-D Vector 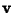 Iff, under Rotation,
Iff, under Rotation,
for 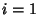 , 2, ...,
, 2, ..., 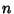 . The Direction Cosines between
. The Direction Cosines between 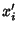 and
and 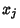 are
are
They satisfy the orthogonality condition
where 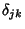 is the Kronecker Delta.
is the Kronecker Delta.
See also Tensor, Vector
© 1996-9 Eric W. Weisstein
1999-05-26
![]() quantities
quantities ![]() are components of an
are components of an ![]() -D Vector
-D Vector ![]() Iff, under Rotation,
Iff, under Rotation,