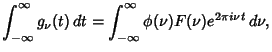The engineering terminology for one use of Fourier Transforms. By breaking up a wave pulse into
its frequency spectrum
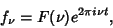 |
(1) |
the entire signal can be written as a sum of contributions from each frequency,
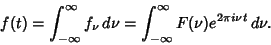 |
(2) |
If the signal is modified in some way, it will become
where 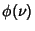 is known as the ``transfer function.'' Fourier Transforming
is known as the ``transfer function.'' Fourier Transforming 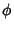 and
and 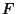 ,
,
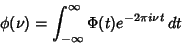 |
(5) |
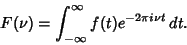 |
(6) |
From the Convolution Theorem,
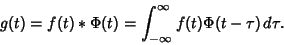 |
(7) |
See also Convolution Theorem, Fourier Transform
© 1996-9 Eric W. Weisstein
1999-05-26