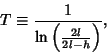The ``temperature'' of a curve 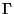 is defined as
is defined as
where 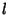 is the length of
is the length of 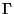 and
and 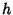 is the length of the Perimeter of the Convex Hull. The
temperature of a curve is 0 only if the curve is a straight line, and increases as the curve becomes more ``wiggly.''
is the length of the Perimeter of the Convex Hull. The
temperature of a curve is 0 only if the curve is a straight line, and increases as the curve becomes more ``wiggly.''
See also Curlicue Fractal
References
Pickover, C. A. Keys to Infinity. New York: Wiley, pp. 164-165, 1995.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is defined as
is defined as