|
|
|
The convex hull of a set of points ![]() is the Intersection of all convex sets containing
is the Intersection of all convex sets containing ![]() . For
. For ![]() points
points
![]() , ...,
, ..., ![]() , the convex hull
, the convex hull ![]() is then given by the expression
is then given by the expression
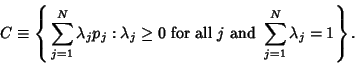
See also Carathéodory's Fundamental Theorem, Cross Polytope, Groemer Packing, Groemer Theorem, Sausage Conjecture, Sylvester's Four-Point Problem
References
Santaló, L. A. Integral Geometry and Geometric Probability. Reading, MA: Addison-Wesley, 1976.