Talbot's Curve

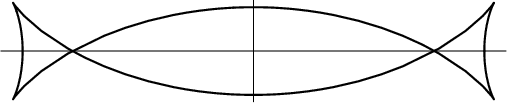
$\begin{figure}\begin{center}\BoxedEPSF{TalbotsCurve.epsf}\end{center}\end{figure}$

A curve investigated by Talbot which is the Negative Pedal Curve of an Ellipse with respect to its center. It has four Cusps and two Nodes, provided the Eccentricity of the Ellipse is greater than $1/\sqrt{2}$ . Its Cartesian Equation is

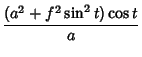$\displaystyle x$	$\textstyle =$	$\displaystyle {(a^2+f^2\sin^2 t)\cos t\over a}$
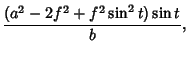$\displaystyle y$	$\textstyle =$	$\displaystyle {(a^2-2f^2+f^2\sin^2 t)\sin t\over b},$

where

is a constant.

References

Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, p. 157, 1967.