|
|
|
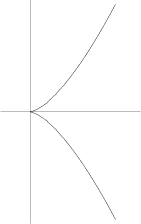
A cusp is a point on a continuous curve where the tangent vector reverses sign as the curve is traversed. A function ![]() has a cusp (also called a Spinode) at a point
has a cusp (also called a Spinode) at a point ![]() if
if ![]() is Continuous at
is Continuous at ![]() and
and
![]() from one side while
from one side while
![]() from the other side, so the curve is Continuous but the Derivative is not. A cusp is a
type of Double Point. The above plot shows the curve
from the other side, so the curve is Continuous but the Derivative is not. A cusp is a
type of Double Point. The above plot shows the curve ![]() , which has a cusp at the Origin.
, which has a cusp at the Origin.
See also Double Cusp, Double Point, Ordinary Double Point, Ramphoid Cusp, Salient Point
References
Walker, R. J. Algebraic Curves. New York: Springer-Verlag, pp. 57-58, 1978.