A second-order Ordinary Differential Equation
where 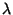 is a constant and
is a constant and 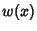 is a known function called either the density or Weighting Function. The
solutions (with appropriate boundary conditions) of
is a known function called either the density or Weighting Function. The
solutions (with appropriate boundary conditions) of 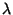 are called Eigenvalues and the
corresponding
are called Eigenvalues and the
corresponding 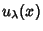 Eigenfunctions. The solutions of this equation satisfy important
mathematical properties under appropriate boundary conditions (Arfken 1985).
Eigenfunctions. The solutions of this equation satisfy important
mathematical properties under appropriate boundary conditions (Arfken 1985).
See also Adjoint Operator, Self-Adjoint Operator
References
Arfken, G. ``Sturm-Liouville Theory--Orthogonal Functions.'' Ch. 9 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 497-538, 1985.
© 1996-9 Eric W. Weisstein
1999-05-26