|
|
|
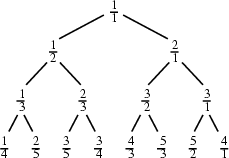
A special type of Binary Tree obtained by starting with the fractions
![]() and
and
![]() and iteratively
inserting
and iteratively
inserting ![]() between each two adjacent fractions
between each two adjacent fractions ![]() and
and ![]() . The result can be arranged in tree form as
illustrated above. The Farey Sequence
. The result can be arranged in tree form as
illustrated above. The Farey Sequence ![]() defines a subtree of the Stern-Brocot tree obtained by pruning off unwanted
branches (Vardi 1991, Graham et al. 1994).
defines a subtree of the Stern-Brocot tree obtained by pruning off unwanted
branches (Vardi 1991, Graham et al. 1994).
See also Binary Tree, Farey Sequence, Ford Circle
References
Brocot, A. ``Calcul des rouages par approximation, nouvelle méthode.'' Revue Chonométrique 6, 186-194, 1860.
Graham, R. L.; Knuth, D. E.; and Patashnik, O.
Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 116-117, 1994.
Stern, M. A. ``Über eine zahlentheoretische Funktion.'' J. reine angew. Math. 55, 193-220, 1858.
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, p. 253, 1991.