|
|
|
The Farey sequence ![]() for any Positive Integer
for any Positive Integer ![]() is the set of irreducible Rational Numbers
is the set of irreducible Rational Numbers ![]() with
with
![]() and
and ![]() arranged in increasing order.
arranged in increasing order.
| (1) | |||
| (2) | |||
| (3) | |||
| (4) | |||
| (5) |
| (6) |
| (7) |
The number of terms ![]() in the Farey sequence for the Integer
in the Farey sequence for the Integer ![]() is
is
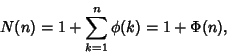 |
(8) |
| (9) |
Ford Circles provide a method of visualizing the Farey sequence. The Farey sequence ![]() defines a
subtree of the Stern-Brocot Tree obtained by pruning unwanted branches (Graham et al. 1994).
defines a
subtree of the Stern-Brocot Tree obtained by pruning unwanted branches (Graham et al. 1994).
See also Ford Circle, Mediant, Rank (Sequence), Stern-Brocot Tree
References
Beiler, A. H. ``Farey Tails.'' Ch. 16 in
Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Conway, J. H. and Guy, R. K. ``Farey Fractions and Ford Circles.'' The Book of Numbers. New York:
Springer-Verlag, pp. 152-154 and 156, 1996.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea,
pp. 155-158, 1952.
Farey, J. ``On a Curious Property of Vulgar Fractions.'' London, Edinburgh and Dublin Phil. Mag. 47, 385, 1816.
Graham, R. L.; Knuth, D. E.; and Patashnik, O.
Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 118-119, 1994.
Guy, R. K. ``Mahler's Generalization of Farey Series.'' §F27 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 263-265, 1994.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Sloane, N. J. A. Sequences
A005728/M0661,
A006842/M0041, and
A006843/M0081
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Sylvester, J. J. ``On the Number of Fractions Contained in Any Farey Series of Which the Limiting Number is Given.''
London, Edinburgh and Dublin Phil. Mag. (5th Series) 15, 251, 1883.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 155, 1991.
![]() Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.
Weisstein, E. W. ``Plane Geometry.'' Mathematica notebook PlaneGeometry.m.
|
|
|
© 1996-9 Eric W. Weisstein