|
|
|
A Hypotrochoid generated by a fixed point on a Circle rolling inside a fixed Circle. It has parametric
equations,
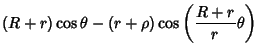 |
(1) | ||
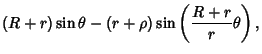 |
(2) |
| (3) | |||
| (4) |
| (5) | |||
| (6) | |||
| (7) | |||
| (8) |
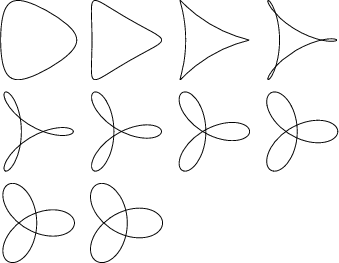
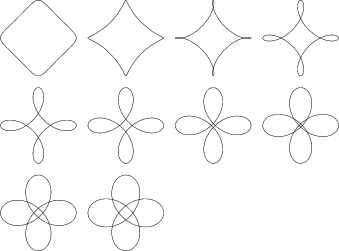


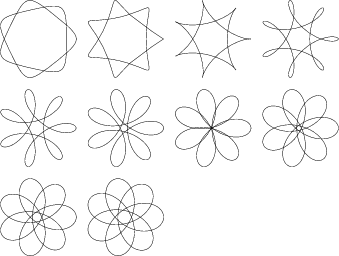
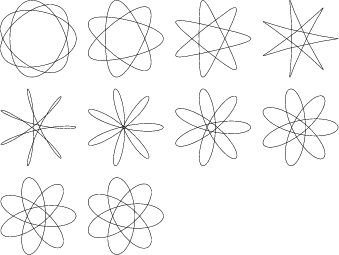
Additional attractive designs such as the following can also be made by superposing individual spirographs.
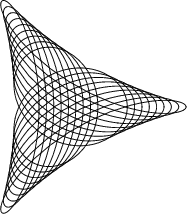
See also Epitrochoid, Hypotrochoid, Maurer Rose, Spirolateral
|
|
|
© 1996-9 Eric W. Weisstein