|
|
|
|
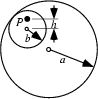
The Roulette traced by a point ![]() attached to a Circle of radius
attached to a Circle of radius ![]() rolling around the inside of a fixed
Circle of radius
rolling around the inside of a fixed
Circle of radius ![]() . The parametric equations for a hypotrochoid are
. The parametric equations for a hypotrochoid are
| (1) | |||
| (2) |
| (3) | |||
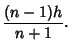 |
(4) |
See also Epitrochoid, Hypocycloid, Spirograph
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 165-168, 1972.
Lee, X. ``Hypotrochoid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Hypotrochoid_dir/hypotrochoid.html
Lee, X. ``Epitrochoid and Hypotrochoid Movie Gallery.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/EpiHypoTMovieGallery_dir/epiHypoTMovieGallery.html
MacTutor History of Mathematics Archive. ``Hypotrochoid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Hypotrochoid.html.