|
|
|
A problem also known as the Points Problem or Unfinished Game. Consider a tournament involving ![]() players
playing the same game repetitively. Each game has a single winner, and denote the number of games won by player
players
playing the same game repetitively. Each game has a single winner, and denote the number of games won by player ![]() at
some juncture
at
some juncture ![]() . The games are independent, and the probability of the
. The games are independent, and the probability of the ![]() th player winning a game is
th player winning a game is ![]() . The
tournament is specified to continue until one player has won
. The
tournament is specified to continue until one player has won ![]() games. If the tournament is discontinued before any
player has won
games. If the tournament is discontinued before any
player has won ![]() games so that
games so that ![]() for
for ![]() , ...,
, ..., ![]() , how should the prize money be shared in order to
distribute it proportionally to the players' chances of winning?
, how should the prize money be shared in order to
distribute it proportionally to the players' chances of winning?
For player ![]() , call the number of games left to win
, call the number of games left to win
![]() the ``quota.'' For two players, let
the ``quota.'' For two players, let ![]() and
and
![]() be the probabilities of winning a single game, and
be the probabilities of winning a single game, and
![]() and
and
![]() be
the number of games needed for each player to win the tournament. Then the stakes should be divided in the ratio
be
the number of games needed for each player to win the tournament. Then the stakes should be divided in the ratio ![]() ,
where
,
where
![$\displaystyle p^a\left[{1+{a\over 1}q+{a(a+1)\over 2!}q^2+\ldots+{a(a+1)\cdots(a+b-2)\over(b-1)!}q^{b-1}}\right]$](s1_897.gif) |
(1) | ||
![$\displaystyle q^b\left[{1+{b\over 1}p+{b(b+1)\over 2!}p^2+\ldots+{b(b+1)\cdots(b+a-2)\over(a-1)!}p^{a-1}}\right]$](s1_899.gif) |
(2) |
If ![]() players have equal probability of winning (``cell probability''), then the chance of player
players have equal probability of winning (``cell probability''), then the chance of player ![]() winning for quotas
winning for quotas ![]() ,
...,
,
..., ![]() is
is
| (3) |
| (4) |
| (5) |
| (6) |
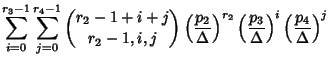 |
|||
| (7) |
See also Dirichlet Integrals
References
Kraitchik, M. ``The Unfinished Game.'' §6.1 in Mathematical Recreations. New York: W. W. Norton,
pp. 117-118, 1942.
Sobel, M. and Frankowski, K. ``The 500th Anniversary of the Sharing Problem (The Oldest Problem in the
Theory of Probability).'' Amer. Math. Monthly 101, 833-847, 1994.
|
|
|
© 1996-9 Eric W. Weisstein