|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Consider the sum
| (1) |
| (2) |
| (3) |
| (4) |
| (5) | |||
| (6) |
| (7) |
A modified sum was considered by Elbert (1973):
| (8) |
| (9) |
| (10) |
| (11) | |||
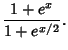 |
(12) |
| (13) |
See also Convex Hull
References
Drinfeljd, V. G. ``A Cyclic Inequality.'' Math. Notes. Acad. Sci. USSR 9, 68-71, 1971.
Elbert, A. ``On a Cyclic Inequality.'' Period. Math. Hungar. 4, 163-168, 1973.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/shapiro/shapiro.html
Mitrinovic, D. S.; Pecaric, J. E.; and Fink, A. M. Classical and New Inequalities in Analysis. New York: Kluwer, 1993.
|
|
|
© 1996-9 Eric W. Weisstein