|
|
|
A generalization of the Gaussian Sum. For ![]() and
and ![]() of opposite Parity (i.e., one is Even and the other is
Odd), Schaar's identity states
of opposite Parity (i.e., one is Even and the other is
Odd), Schaar's identity states
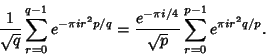
See also Gaussian Sum
References
Evans, R. and Berndt, B. ``The Determination of Gauss Sums.'' Bull. Amer. Math. Soc. 5, 107-129, 1981.