Let 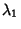 , ...,
, ...,
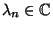 be linearly independent over the Rationals
be linearly independent over the Rationals 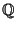 ,
then
,
then
has Transcendence degree at least 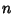 over
over 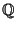 . Schanuel's conjecture is a
generalization of the Lindemann-Weierstraß Theorem. If the conjecture is true,
then it follows that
. Schanuel's conjecture is a
generalization of the Lindemann-Weierstraß Theorem. If the conjecture is true,
then it follows that 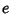 and
and 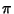 are algebraically independent. Mcintyre (1991) proved that the truth of Schanuel's
conjecture also guarantees that there are no unexpected exponential-algebraic relations on the Integers
are algebraically independent. Mcintyre (1991) proved that the truth of Schanuel's
conjecture also guarantees that there are no unexpected exponential-algebraic relations on the Integers
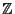 (Marker 1996).
(Marker 1996).
See also Constant Problem
References
Macintyre, A. ``Schanuel's Conjecture and Free Exponential Rings.'' Ann. Pure Appl. Logic 51, 241-246, 1991.
Marker, D. ``Model Theory and Exponentiation.'' Not. Amer. Math. Soc. 43, 753-759, 1996.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , ...,
, ...,
![]() be linearly independent over the Rationals
be linearly independent over the Rationals ![]() ,
then
,
then