|
|
|
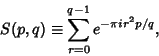 |
(1) |
| (2) |
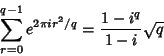 |
(3) |
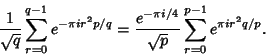 |
(4) |
See also Kloosterman's Sum, Schaar's Identity, Singular Series
References
Evans, R. and Berndt, B. ``The Determination of Gauss Sums.'' Bull. Amer. Math. Soc. 5, 107-129, 1981.
Katz, N. M. Gauss Sums, Kloosterman Sums, and Monodromy Groups. Princeton, NJ: Princeton University Press, 1987.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 132-134, 1994.