|
|
|
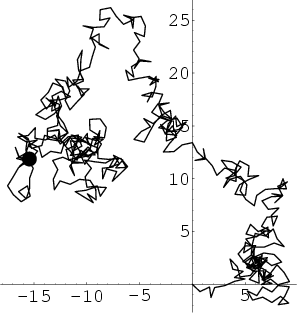
In a Plane, consider a sum of ![]() 2-D Vectors with random orientations. Use Phasor
notation, and let the phase of each Vector be Random. Assume
2-D Vectors with random orientations. Use Phasor
notation, and let the phase of each Vector be Random. Assume ![]() unit steps are taken
in an arbitrary direction (i.e., with the angle
unit steps are taken
in an arbitrary direction (i.e., with the angle ![]() uniformly distributed in
uniformly distributed in ![]() and not on a
Lattice), as illustrated above. The position
and not on a
Lattice), as illustrated above. The position ![]() in the Complex Plane after
in the Complex Plane after ![]() steps is then given by
steps is then given by
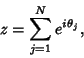 |
(1) |
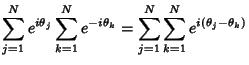 |
|||
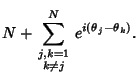 |
(2) |
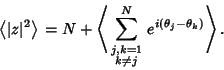 |
(3) |
| (4) |
| (5) |
| (6) |
| (7) |
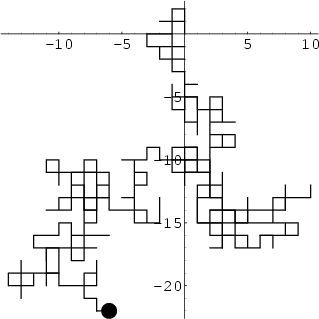
Amazingly, it has been proven that on a 2-D Lattice, a random walk has unity probability of reaching any point (including the starting point) as the number of steps approaches Infinity.
See also Pólya's Random Walk Constants, Random Walk--1-D, Random Walk--3-D
|
|
|
© 1996-9 Eric W. Weisstein