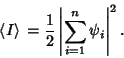The representation, beloved of engineers and physicists, of a Complex Number in terms of a Complex exponential
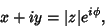 |
(1) |
where i (called j by engineers) is the Imaginary Number and the Modulus and Argument (also called Phase) are
Here, 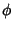 is the counterclockwise Angle from the Positive Real axis. In the degenerate
case when
is the counterclockwise Angle from the Positive Real axis. In the degenerate
case when 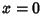 ,
,
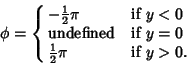 |
(4) |
It is trivially true that
![\begin{displaymath}
\sum_i \Re[\psi_i] = \Re\left[{\sum_i \psi_i}\right].
\end{displaymath}](p1_1437.gif) |
(5) |
Now consider a Scalar Function
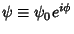 . Then
. Then
Look at the time averages of each term,
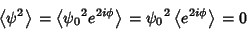 |
(7) |
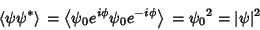 |
(8) |
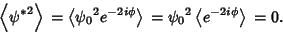 |
(9) |
Therefore,
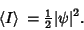 |
(10) |
Consider now two scalar functions
Then
In general,
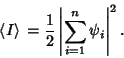 |
(15) |
See also Affix, Argument (Complex Number), Complex Multiplication, Complex Number, Modulus
(Complex Number), Phase
© 1996-9 Eric W. Weisstein
1999-05-26
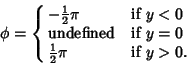
![\begin{displaymath}
\sum_i \Re[\psi_i] = \Re\left[{\sum_i \psi_i}\right].
\end{displaymath}](p1_1437.gif)