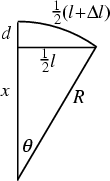
Given a straight segment of track of length 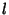 , add a small segment
, add a small segment 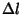 so that
the track bows into a circular Arc. Find the maximum displacement
so that
the track bows into a circular Arc. Find the maximum displacement 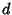 of the bowed
track. The Pythagorean Theorem gives
of the bowed
track. The Pythagorean Theorem gives
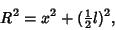 |
(1) |
But 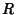 is simply
is simply 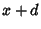 , so
, so
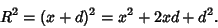 |
(2) |
Solving (1) and (2) for 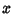 gives
gives
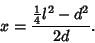 |
(3) |
Expressing the length of the Arc in terms of the central angle,
But 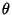 is given by
is given by
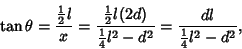 |
(5) |
so plugging 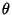 in gives
in gives
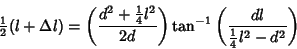 |
(6) |
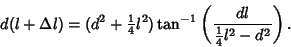 |
(7) |
For 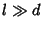 ,
,
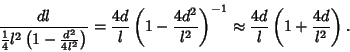 |
(8) |
Therefore,
Keeping only terms to order 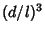 ,
,
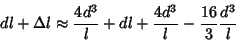 |
(10) |
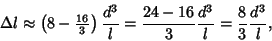 |
(11) |
so
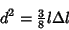 |
(12) |
and
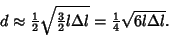 |
(13) |
If we take
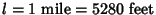 and
and 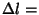 1 foot, then
1 foot, then
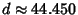 feet.
feet.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() , add a small segment
, add a small segment ![]() so that
the track bows into a circular Arc. Find the maximum displacement
so that
the track bows into a circular Arc. Find the maximum displacement ![]() of the bowed
track. The Pythagorean Theorem gives
of the bowed
track. The Pythagorean Theorem gives
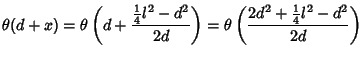
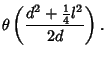
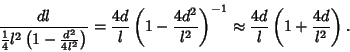
![$\displaystyle (d^2+{\textstyle{1\over 4}}l^2)\left\{{{4d\over l}\left({1+{4d^2\...
...{1\over 3}\left[{{4d\over l}\left({1+{4d^2\over l^2}}\right)}\right]^3}\right\}$](r_313.gif)
![$\displaystyle (d^2+{\textstyle{1\over 4}}l^2)\left[{{4d\over l}+{16d^3\over l^3}-{1\over 3}\left({4d\over l}\right)^3 \left({1+3 {4d^2\over l^2}}\right)}\right].$](r_314.gif)