|
|
|
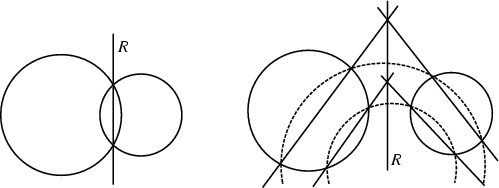
The Locus of points of equal Power with respect to two nonconcentric
Circles which is Perpendicular to the line of centers (the Chordal Theorem; Dörrie 1965).
Let the circles have Radii ![]() and
and ![]() and their centers be separated by a distance
and their centers be separated by a distance ![]() . If the
Circles intersect in two points, then the radical line is the line passing through the points of
intersection. If not, then draw any two Circles which cut each original Circle twice. Draw lines
through each pair of points of intersection of each Circle. The line connecting their two points of intersection is
then the radical line.
. If the
Circles intersect in two points, then the radical line is the line passing through the points of
intersection. If not, then draw any two Circles which cut each original Circle twice. Draw lines
through each pair of points of intersection of each Circle. The line connecting their two points of intersection is
then the radical line.
The radical line is located at distances
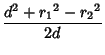 |
(1) | ||
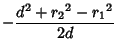 |
(2) |
| (3) |
The radical line of any two Polar Circles is the Altitude from the third vertex.
See also Chordal Theorem, Coaxal Circles, Inverse Points, Inversion, Power (Circle), Radical Center
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 31-34, 1967.
Dixon, R. Mathographics. New York: Dover, p. 68, 1991.
Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, p. 153, 1965.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 28-34 and 176-177, 1929.