|
|
|
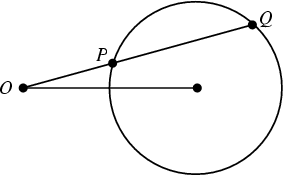
The Power of the two points ![]() and
and ![]() with respect to a Circle is defined by
with respect to a Circle is defined by
Let ![]() be the Radius of a Circle and
be the Radius of a Circle and ![]() be the distance between a point
be the distance between a point ![]() and the circle's center. Then the
Power of the point
and the circle's center. Then the
Power of the point ![]() relative to the circle is
relative to the circle is
The Locus of points having Power ![]() with regard to a fixed Circle of Radius
with regard to a fixed Circle of Radius ![]() is a
Concentric Circle of Radius
is a
Concentric Circle of Radius ![]() . The Chordal Theorem states that the Locus of
points having equal Power with respect to two given nonconcentric Circles is a line called the
Radical Line (or Chordal; Dörrie 1965).
. The Chordal Theorem states that the Locus of
points having equal Power with respect to two given nonconcentric Circles is a line called the
Radical Line (or Chordal; Dörrie 1965).
See also Chordal Theorem, Coaxal Circles, Inverse Points, Inversion Circle, Inversion Radius, Inversive Distance, Radical Line
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 27-31, 1967.
Dixon, R. Mathographics. New York: Dover, p. 68, 1991.
Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, p. 153, 1965.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, pp. 28-34, 1929.
Pedoe, D. Circles: A Mathematical View, rev. ed. Washington, DC: Math. Assoc. Amer., pp. xxii-xxiv, 1995.
|
|
|
© 1996-9 Eric W. Weisstein