The q-Analog of the Sine function, as advocated by R. W. Gosper, is defined by
where
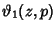 is a Theta Function and
is a Theta Function and 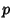 is defined via
is defined via
This is a period 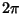 , Odd Function of unit amplitude with double and triple angle formulas and addition formulas which
are analogous to ordinary Sine and Cosine. For example,
, Odd Function of unit amplitude with double and triple angle formulas and addition formulas which
are analogous to ordinary Sine and Cosine. For example,
where 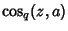 is the q-Cosine, and
is the q-Cosine, and 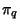 is q-Pi.
is q-Pi.
See also q-Cosine, q-Factorial
References
Gosper, R. W. ``Experiments and Discoveries in 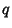 -Trigonometry.'' Unpublished manuscript.
-Trigonometry.'' Unpublished manuscript.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() -Trigonometry.'' Unpublished manuscript.
-Trigonometry.'' Unpublished manuscript.