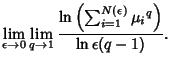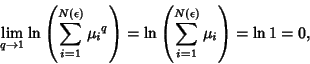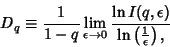 |
(1) |
where
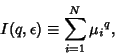 |
(2) |
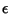 is the box size, and
is the box size, and 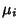 is the Natural Measure. If
is the Natural Measure. If 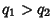 , then
, then
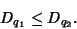 |
(3) |
The Capacity Dimension (a.k.a. Box Counting Dimension) is given by 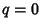 ,
,
![\begin{displaymath}
D_0 = {1\over 1-0} \lim_{\epsilon\to 0} {\ln\left({\sum_{i=1...
...= - \lim_{\epsilon\to 0} {\ln[N(\epsilon)]\over \ln \epsilon}.
\end{displaymath}](q_53.gif) |
(4) |
If all 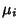 s are equal, then the Capacity Dimension is obtained for any
s are equal, then the Capacity Dimension is obtained for any 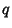 . The Information Dimension
is defined by
. The Information Dimension
is defined by
But
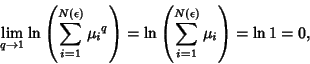 |
(6) |
so use L'Hospital's Rule
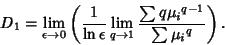 |
(7) |
Therefore,
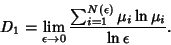 |
(8) |
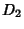 is called the Correlation Dimension. The
is called the Correlation Dimension. The 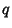 -dimensions satisfy
-dimensions satisfy
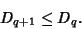 |
(9) |
See also Fractal Dimension
© 1996-9 Eric W. Weisstein
1999-05-25
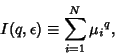
![\begin{displaymath}
D_0 = {1\over 1-0} \lim_{\epsilon\to 0} {\ln\left({\sum_{i=1...
...= - \lim_{\epsilon\to 0} {\ln[N(\epsilon)]\over \ln \epsilon}.
\end{displaymath}](q_53.gif)
![$\displaystyle \lim_{q\to 1} D_q = \lim_{q\to 1}{\lim_{\epsilon\to 0}{\ln\left[{\sum_{i=1}^{N(\epsilon)}{\mu_i}^q}\right]\over -\ln\epsilon}\over {1-q}}$](q_55.gif)