|
|
|
Let lim stand for the Limit ![]() ,
,
![]() ,
,
![]() ,
,
![]() , or
, or
![]() , and suppose that lim
, and suppose that lim ![]() and lim
and lim ![]() are both Zero or are both
are both Zero or are both ![]() . If
. If
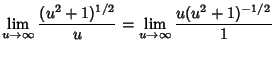 |
|||
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 13, 1972.
L'Hospital, G. de L'analyse des infiniment petits pour l'intelligence des lignes courbes. 1696.