|
|
|
A Quadratic Form ![]() is said to be positive definite if
is said to be positive definite if ![]() for
for
![]() . A
Real Quadratic Form in
. A
Real Quadratic Form in ![]() variables is positive definite Iff its canonical form is
variables is positive definite Iff its canonical form is
| (1) |
| (2) |
| (3) |
A Quadratic Form
![]() is positive definite Iff every Eigenvalue of
is positive definite Iff every Eigenvalue of
![]() is Positive. A Quadratic Form
is Positive. A Quadratic Form
![]() with
with
![]() a Hermitian Matrix is
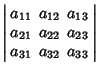
positive definite if all the principal minors in the top-left corner of
a Hermitian Matrix is
positive definite if all the principal minors in the top-left corner of
![]() are Positive, in other words
are Positive, in other words
| (4) | |||
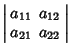 |
(5) | ||
 |
(6) |
See also Indefinite Quadratic Form, Positive Semidefinite Quadratic Form
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1106, 1979.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 38, 1983.
|
|
|
© 1996-9 Eric W. Weisstein